1. Decimal to fraction part:.6 = 6 / 10 Fraction in 2 point simple form: 60/100 = 6/10 = 3/5. Use the level of precision to understand and customize how decimal 0.6 is broken down into a fraction. The page also includes 2-3D graphical representations of 0.6 as a fraction, the different types of fractions, and what type of fraction 0.6 is when.
2. Decimals can be renamed as other decimals or fractions. For example, 800/1000 or 0.800 can be renamed as 80/100 or 0.80. It can also be renamed as 8/10 or 0.8 Take note that 0.5 or 0.50 or 0.500 are all equal to 1/2 0.25 or 0.250 are both equal 1/4 0.75 and 0.750 are equal to 3/4. We can use a thousands grid to model decimals.
3. The following table demonstrates the results of rounding some negative and positive numbers in conjunction with round-to-nearest modes. The precision used to round the numbers is zero, which means the number after the decimal point affects the rounding operation. For example, for the number -2.5, the digit after the decimal point is 5.

• Windowmizer 5 0 6 Decimal Fractions
• Windowmizer 5 0 6 Decimal Percent
• Windowmizer 5 0 6 Decimal Fraction

To use this decimal to hex converter tool, you have to type a decimal value like 79 into the left field below, and then hit the Convert button. Therefore, you can convert up to 19 decimal characters (max. value of 9223372036854775807) to hex.

Decimal to hex conversion result in base numbers

Decimal System

The decimal numeral system is the most commonly used and the standard system in daily life. It uses the number 10 as its base (radix). Therefore, it has 10 symbols: The numbers from 0 to 9; namely 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.

As one of the oldest known numeral systems, the decimal numeral system has been used by many ancient civilizations. The difficulty of representing very large numbers in the decimal system was overcome by the Hindu–Arabic numeral system. The Hindu-Arabic numeral system gives positions to the digits in a number and this method works by using powers of the base 10; digits are raised to the n^th power, in accordance with their position.

REAL FIXED BINARY (31,0) FLOAT4: A 4-byte single-precision floating-point number: REAL FLOAT BINARY (21) or REAL FLOAT DECIMAL (6) FLOAT8: An 8-byte double-precision floating-point number: REAL FLOAT BINARY (53) or REAL FLOAT DECIMAL (16) FLOAT16: A 16-byte extended-precision floating-point number: REAL FLOAT DECIMAL (33) or REAL FLOAT BINARY.

For instance, take the number 2345.67 in the decimal system:

• The digit 5 is in the position of ones (10⁰, which equals 1),
• 4 is in the position of tens (10¹)
• 3 is in the position of hundreds (10²)
• 2 is in the position of thousands (10³)
• Meanwhile, the digit 6 after the decimal point is in the tenths (1/10, which is 10^-1) and 7 is in the hundredths (1/100, which is 10^-2) position
• Thus, the number 2345.67 can also be represented as follows: (2 * 10³) + (3 * 10²) + (4 * 10¹) + (5 * 10⁰) + (6 * 10^-1) + (7 * 10^-2)

Hexadecimal System (Hex System)

The hexadecimal system (shortly hex), uses the number 16 as its base (radix). As a base-16 numeral system, it uses 16 symbols. These are the 10 decimal digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) and the first six letters of the English alphabet (A, B, C, D, E, F). The letters are used because of the need to represent the values 10, 11, 12, 13, 14 and 15 each in one single symbol.

Hex is used in mathematics and information technologies as a more friendly way to represent binary numbers. Each hex digit represents four binary digits; therefore, hex is a language to write binary in an abbreviated form.

Four binary digits (also called nibbles) make up half a byte. This means one byte can carry binary values from 0000 0000 to 1111 1111. In hex, these can be represented in a friendlier fashion, ranging from 00 to FF.

In html programming, colors can be represented by a 6-digit hexadecimal number: FFFFFF represents white whereas 000000 represents black.

How to Convert Decimal to Hex

Decimal to hexadecimal conversion can be achieved by applying the repeated division and remainder algorithm. Simply put, the decimal number is repeatedly divided by the radix 16. In between these divisions, the remainders give the hex equivalent in reverse order.

Here is how to convert decimal to hex step by step:

• Step 1: If the given decimal number is less than 16, the hex equivalent is the same. Remembering that the letters A, B, C, D, E and F are used for the values 10, 11, 12, 13, 14 and 15, convert accordingly. For example, the decimal number 15 will be F in hex.
• Step 2: If the given decimal number is 16 or greater, divide the number by 16.
• Step 3: Write down the remainder.
• Step 4: Divide the part before the decimal point of your quotient by 16 again. Write down the remainder.
• Step 5: Continue this process of dividing by 16 and noting the remainders until the last decimal digit you are left with is less than 16.
• Step 6: When the last decimal digit is less than 16, the quotient will be less than 0 and the remainder will be the digit itself.
• Step 7: The last remainder you get will be the most significant digit of your hex value while the first remainder from Step 3 is the least significant digit. Therefore, when you write the remainders in reverse order - starting at the bottom with the most significant digit and going to the top- you will reach the hex value of the given decimal number.

Now, let’s apply these steps to, for example, the decimal number (501)₁₀

Decimal to Hex Conversion Examples

Example 1: (4253)₁₀ = (109D)₁₆

Example 2: (16)₁₀ = (10)₁₆

Example 3: (45)₁₀ = (2D)₁₆

Decimal to Hexadecimal Conversion Table

Decimal	Hexadecimal
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10	A
11	B
12	C
13	D
14	E
15	F
16	10
17	11
18	12
19	13
20	14
21	15
22	16
23	17
24	18
25	19
26	1A
27	1B
28	1C
29	1D
30	1E
31	1F
32	20
33	21
34	22
35	23
36	24
37	25
38	26
39	27
40	28
41	29
42	2A
43	2B
44	2C
45	2D
46	2E
47	2F
48	30
49	31
50	32
51	33
52	34
53	35
54	36
55	37
56	38
57	39
58	3A
59	3B
60	3C
61	3D
62	3E
63	3F
64	40
65	41
66	42
67	43
68	44
69	45
70	46
71	47
72	48
73	49
74	4A
75	4B
76	4C
77	4D
78	4E
79	4F
80	50

Decimal	Hexadecimal
81	51
82	52
83	53
84	54
85	55
86	56
87	57
88	58
89	59
90	5A
91	5B
92	5C
93	5D
94	5E
95	5F
96	60
97	61
98	62
99	63
100	64
101	65
102	66
103	67
104	68
105	69
106	6A
107	6B
108	6C
109	6D
110	6E
111	6F
112	70
113	71
114	72
115	73
116	74
117	75
118	76
119	77
120	78
121	79
122	7A
123	7B
124	7C
125	7D
126	7E
127	7F
128	80
129	81
130	82
131	83
132	84
133	85
134	86
135	87
136	88
137	89
138	8A
139	8B
140	8C
141	8D
142	8E
143	8F
144	90
145	91
146	92
147	93
148	94
149	95
150	96
151	97
152	98
153	99
154	9A
155	9B
156	9C
157	9D
158	9E
159	9F
160	A0

Decimal	Hexadecimal
161	A1
162	A2
163	A3
164	A4
165	A5
166	A6
167	A7
168	A8
169	A9
170	AA
171	AB
172	AC
173	AD
174	AE
175	AF
176	B0
177	B1
178	B2
179	B3
180	B4
181	B5
182	B6
183	B7
184	B8
185	B9
186	BA
187	BB
188	BC
189	BD
190	BE
191	BF
192	C0
193	C1
194	C2
195	C3
196	C4
197	C5
198	C6
199	C7
200	C8
201	C9
202	CA
203	CB
204	CC
205	CD
206	CE
207	CF
208	D0
209	D1
210	D2
211	D3
212	D4
213	D5
214	D6
215	D7
216	D8
217	D9
218	DA
219	DB
220	DC
221	DD
222	DE
223	DF
224	E0
225	E1
226	E2
227	E3
228	E4
229	E5
230	E6
231	E7
232	E8
233	E9
234	EA
235	EB
236	EC
237	ED
238	EE
239	EF
240	F0

Decimal	Hexadecimal
241	F1
242	F2
243	F3
244	F4
245	F5
246	F6
247	F7
248	F8
249	F9
250	FA
251	FB
252	FC
253	FD
254	FE
255	FF
256	100
257	101
258	102
259	103
260	104
261	105
262	106
263	107
264	108
265	109
266	10A
267	10B
268	10C
269	10D
270	10E
271	10F
272	110
273	111
274	112
275	113
276	114
277	115
278	116
279	117
280	118
281	119
282	11A
283	11B
284	11C
285	11D
286	11E
287	11F
288	120
289	121
290	122
291	123
292	124
293	125
294	126
295	127
296	128
297	129
298	12A
299	12B
300	12C
301	12D
302	12E
303	12F
304	130
305	131
306	132
307	133
308	134
309	135
310	136
311	137
312	138
313	139
314	13A
315	13B
316	13C
317	13D
318	13E
319	13F
320	140

-->

Definition

Specifies how mathematical rounding methods should process a number that is midway between two numbers.

Windowmizer 5 0 6 Decimal Fractions

Inheritance

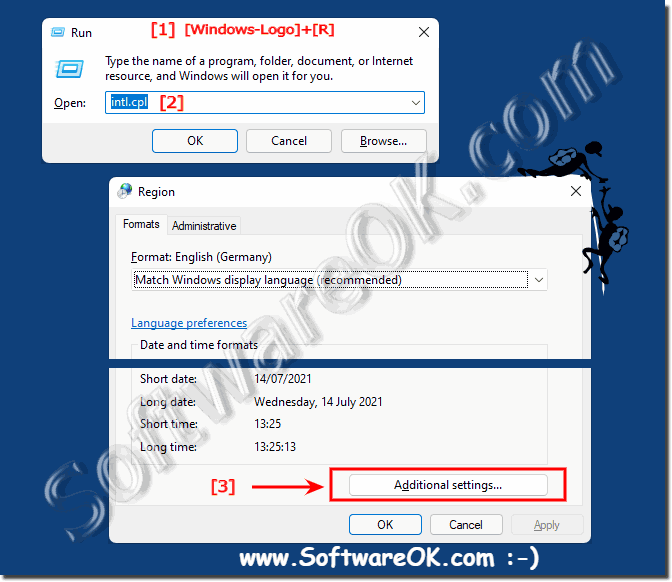
Attributes

Fields

AwayFromZero	1	Round to nearest mode: when a number is halfway between two others, it is rounded toward the nearest number that is away from zero.
ToEven	0	Round to nearest mode: when a number is halfway between two others, it is rounded toward the nearest even number.
ToNegativeInfinity	3	Directed mode: the number is rounded down, with the result closest to and no greater than the infinitely precise result.
ToPositiveInfinity	4	Directed mode: the number is rounded up, with the result closest to and no less than the infinitely precise result.
ToZero	2	Directed mode: the number is rounded toward zero, with the result closest to and no greater in magnitude than the infinitely precise result.

Examples

The following example demonstrates the Math.Round method in conjunction with the MidpointRounding enumeration:

Remarks

Use MidpointRounding with appropriate overloads of Math.Round to provide more control of the rounding process.

Round to nearest

A round-to-nearest operation takes an original number with an implicit or specified precision; examines the next digit, which is at that precision plus one; and returns the nearest number with the same precision as the original number. For positive numbers, if the next digit is from 0 through 4, the nearest number is toward negative infinity. If the next digit is from 6 through 9, the nearest number is toward positive infinity. For negative numbers, if the next digit is from 0 through 4, the nearest number is toward positive infinity. If the next digit is from 6 through 9, the nearest number is toward negative infinity.

In the previous cases, the MidpointRounding.AwayFromZero and MidpointRounding.ToEven do not affect the result of the rounding operation. However, if the next digit is 5, which is the midpoint between two possible results, and all remaining digits are zero or there are no remaining digits, the nearest number is ambiguous. In this case, the round-to-nearest modes in MidpointRounding enable you to specify whether the rounding operation returns the nearest number away from zero or the nearest even number.

The following table demonstrates the results of rounding some negative and positive numbers in conjunction with round-to-nearest modes. The precision used to round the numbers is zero, which means the number after the decimal point affects the rounding operation. For example, for the number -2.5, the digit after the decimal point is 5. Because that digit is the midpoint, you can use a MidpointRounding value to determine the result of rounding. If AwayFromZero is specified, -3 is returned because it is the nearest number away from zero with a precision of zero. If ToEven is specified, -2 is returned because it is the nearest even number with a precision of zero.

Original number	AwayFromZero	ToEven
3.5	4	4
2.8	3	3
2.5	3	2
2.1	2	2
-2.1	-2	-2
-2.5	-3	-2
-2.8	-3	-3
-3.5	-4	-4

Directed rounding

A directed rounding operation takes an original number with an implicit or specified precision and returns the next number closest to some predefined one with the same precision as the original number. Directed modes on MidpointRounding control toward which predefined number the rounding is performed.

The following table demonstrates the results of rounding some negative and positive numbers in conjunction with directed rounding modes. The precision used to round the numbers is zero, which means the number before the decimal point is affected by the rounding operation.

Windowmizer 5 0 6 Decimal Percent

Original number	ToNegativeInfinity	ToPositiveInfinity	ToZero
2.8	2	3	2
2.5	2	3	2
2.1	2	3	2
-2.1	-3	-2	-2
-2.5	-3	-2	-2
-2.8	-3	-2	-2

Windowmizer 5 0 6 Decimal Fraction

Applies to